Generative and Discriminative Machine Learning Models

Table of Contents:

• Generative vs. discriminative models
• Generative vs. discriminative algorithms
• Generative model written in formal way
• Discriminative model written in formal way
• Bayes Optimal Classifier to get the single prediction
• Discriminative model as a function
• Modeling the Distribution (Generative modeling)

There are few different types machine learning models may fit in:

• parametric vs. non-parametric models
• supervised, unsupervised, semi-supervised
• classification or regression models
• generative or discriminative models

Let’s explain the difference between generative and discriminative models.

Generative vs. discriminative models

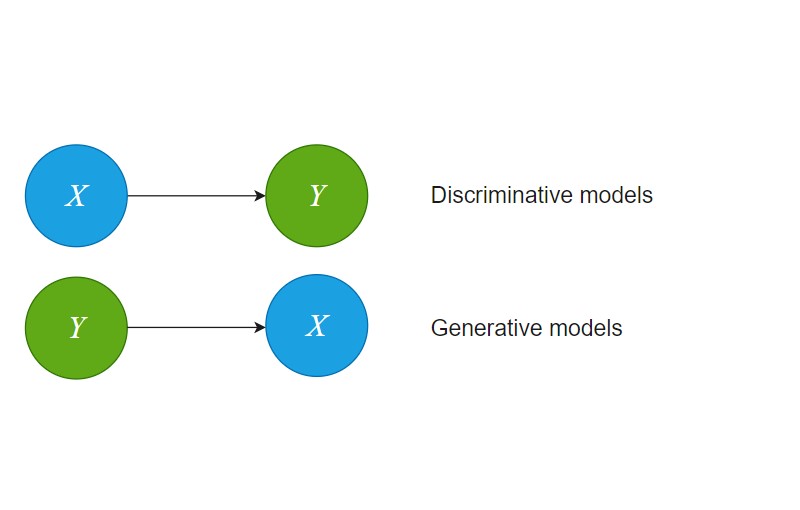
Generative model learns the probability distribution of the observed data.

Example of a generative machine learning model is Naive Bayes. For instance this algorithm was used in the early NLP days for text classification.

Naive Bayes can predict multiple classes based on inputs features. The name “Naive Bayes” was given because of the assumption the algorithm has:

In Naive Bayes features are independent (actually i.i.d. = independent and identically distributed random variables).

In general case features may not be independent.

Discriminative model learns either the hard or the soft boundary between the classes.

Typical examples of discriminative machine learning models are: Logistic Regression, SVM (Support Vector Machines), all decision tree based models, etc.

Generative vs. discriminative algorithms

Discriminative algorithm say given all measures about the human will tell you if that human is a male or female.

Generative algorithm will generate a human given the gender.

In here “gender” is a feature. In general, generative algorithms generate a human based on the features given.

What’s great about generative models: they can create new data.

Generative model written in formal way

Having the features: $X={x_1, x_2, \dots, x_n}$ and label $Y=y$, we can define joint probability $P(Y,X) = P(y,x_1,x_2, \dots, x_n)$

Generative models task is to learn joint probability: $P(X,Y)$ , which in case there are no labels is just $P(X)$. Here $Y$ is the target variable and $X$ is the observable variable.

We can read simple $P(X,Y)$ as: generative model learns the distribution of the data and tells you how likely a given example is.

If we rewrite this joint probability:

$P(X,Y) = P(X \mid Y) P(Y)$

We can read $P(X \mid Y)$ as probability of $X$ given label $Y$.

$P(Y)$ or $p(Y)$ denotes the probability. We use small $p$ for probability of continuous distributions and $P$ for discrete distributions.

Discriminative model written in formal way

Discriminative models learns conditional probability: $P(Y \mid X=x)$.

We may try to learn this probability distribution or to estimate it.

As the return from the discriminative model we may get a probability, but in general case models may not return probability. The return can be a label.

For instance, vanilla SVM models trained to recognize a pedestrian may only return pedestrian or no without providing any probability info.

That model would not be perfect. We would rather like to know the probability of being a pedestrian or not.

Logistic regression models can be used to return the probability of being pedestrian which sounds like a better solution for self-driving cars for instance.

Both generative and discriminative models can generate probabilities, but sometimes they can just generate labels.

Discriminative model can generate probability that an instance belongs to a class.

Generative models can generate probability of an instance, but also probability if the instance belongs to a certain class.

Bayes Optimal Classifier to get the single prediction

When you know the distribution $P(Y \mid X)$ you may use Bayes Optimal classifier to get the prediction for the new data.

Since Bayes Optimal classifier picks the most likely $Y$ for the given $X$ you can use it to determine the most probable prediction for a new data input.

In practice Bayes Optimal classifier may be computationally expensive or even intractable to calculate. Then you will use either Naive Bayes simplification or Gibbs sampling algorithm to approximate the outcome.

Discriminative model as a function

Discriminative model may not learn the $P(Y \mid X)$ because this may be hard. Why to learn the whole distribution when we can just learn the function to get the most likely label:

\[f(X) = \underset{y}{\operatorname{arg\,max}} P(X \mid Y=y)\]

The function will allays return a single label.

If we have probability distribution $P(Y \mid X)$ we can always determine function $f(X)$.

KNN is an example of a discriminative model that works exactly as a function $f(X)$.

Modeling the Distribution (Generative modeling)

Bayes Optimal classifier can help us predict the label once we know the input data and the probability distribution $P$.

Still the question remains: Can we get a machine learning model if we know the distribution ?

To learn the model from the distribution we have two approaches and one formula:

• Maximum a Posteriori (MAP), a Bayesian method
• Maximum Likelihood Estimation (MLE), a frequentist method.

\[P(\theta \mid X) = P(X \mid \theta)P(\theta)\]

Often the terminology for “find a model” is “find a hypothesis”.

Both the methods will search the model that best fits the training data.