k-means clustering

Table of Contents:

• k-means is non-parametric, unsupervised and generative
• Clustering vs. segmentation (classification)
• k-means clustering vs. KNN
• The number of clusters $k$
• Centroids
• No bias
• Algorithm steps
• Few important question about k-means
  • How to choose $k$?
  • How to calculate the k-means clustering error?
  • Hard vs. soft clustering difference
  • K-means algorithm providing bad results

k-means is non-parametric, unsupervised and generative

Let’s explain closely what this means.

• k-means clustering is unsupervised algorithm because data points are unlabeled.
• k-means clustering is generative model because we will learn the cluster distribution, not the cluster boundaries.
• it is also non-parametric method for clustering data, meaning we don’t assume data distribution a priori. Data distribution is determined from the data.

Clustering vs. segmentation (classification)

Even though both clustering and segmentation produce classes, clustering does not imply the number of clusters, their names, etc. Segmentation implies prior knowledge about classes, including their number and names.

You can call classes either groups, clusters or segments.

k-means clustering vs. KNN

Often people mix up k-means clustering task with KNN because of the leading K letter.

KNN is supervised classification task where the outcome is a known class. K-means clustering represents an unsupervised algorithm, used for clustering.

The number of clusters $k$

The variable $k$ represents the number of groups or clusters the algorithm will create. This value $k$ is something we define arbitrarily and it should be smaller than the number of data points $n$.

Centroids

Every cluster will have associated data points. A mean data point of a cluster is called a centroid. A centroid is calculated every time except at the start when centroids are set as random data points. You can think centroid represents a specific collection of features.

No bias

The k-means algorithm has no bias. The algorithm creates clusters automatically with no predefined assumptions.

An unbiased estimator has the property that in an infinite number of trials its average value will equal the true value. The quality of an unbiased estimator is characterized by the variance of the estimator. The smaller the variance the more precise the estimator is.

Algorithm steps

There are three steps of k-means algorithm:

• data assignment: split anonymous data sets into k clusters by randomly selecting k data points for the centroids.

• centroid update: recalculate centroids as the mean of all data points of a cluster.

• repeat assignment and update steps until some criteria, usually when centroids don’t move any more.

Few important question about k-means

How to choose $k$?

The best number of clusters $k$ will have the greatest separation (distance) and we need to compute it from the data.

For different values of the number $k$ we determine the corresponding validation error. We pick the $k$ with the smallest validation error.

How to calculate the k-means clustering error?

First we calculate the centroids:

\[c_1 = \frac{x_1+x_2+ \cdots + x_n}{n}\]

where $x_1, x_2, \cdots ,x_n$ are data points.

Then we calculate the errors per cluster based on centroids.

\[e_1 = \sum_{i=1}^n \mid \mid x_i - c_i \mid \mid\]

The total error is the sum of errors from all the centroids:

\[J = \sum_{j=1}^k \sum_{i=1}^n \mid \mid x_i^{(j)} - c_j \mid \mid ^2\]

Hard vs. soft clustering difference

k-means is what is known as hard clustering. Each data point is part of a single cluster.

Soft clustering is a probability approach. Probability is assigned for the data point to belong to a certain cluster. GMM (Gaussian Mixture Models) is an example of such clustering.

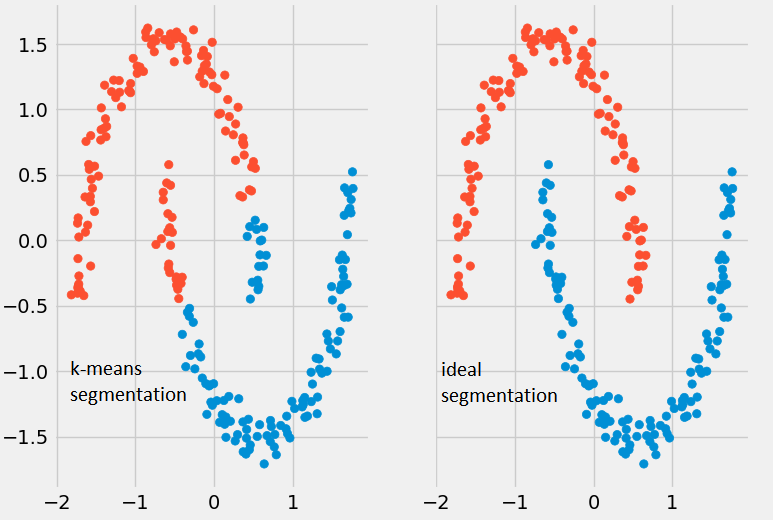
K-means algorithm providing bad results

k-means clustering will provide bad results when:

• the data contains outliers
• data is low dimensional