How logistic regression works?

Sigmoid function inside

Let’s have a function:

$Sig(x)=\Large{\frac{e^x}{1 + e^{x}}}$

that looks like this:

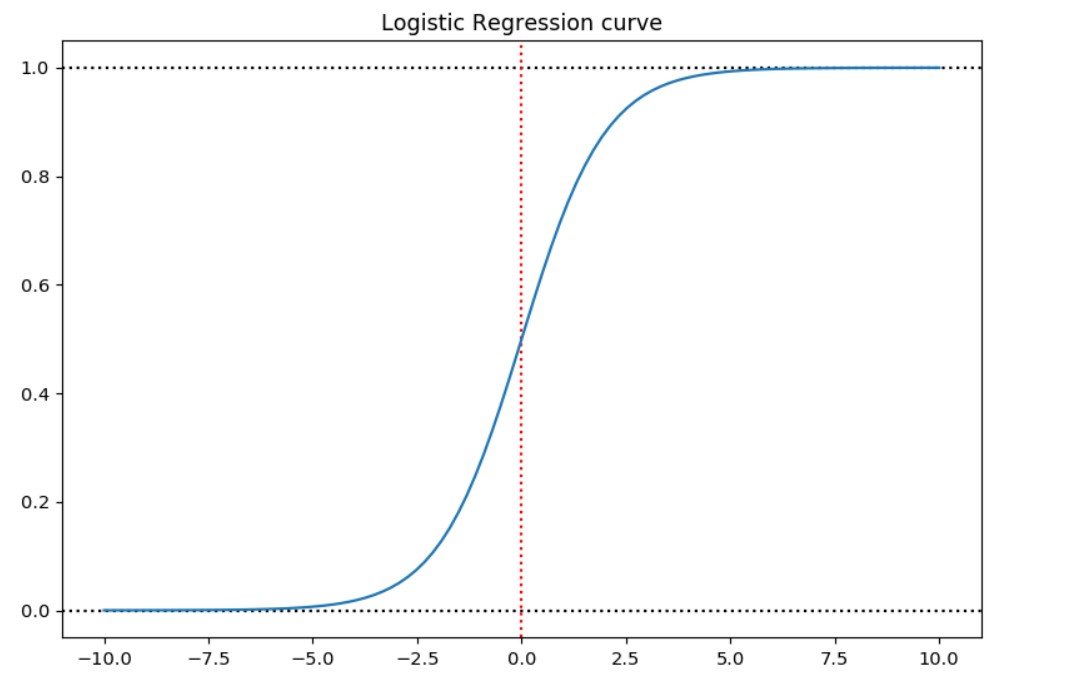
It has values in between the range 0 and 1 for any input from -Inf, to Inf.

import numpy as np
from matplotlib import pyplot as plt
x=np.linspace(-10, 10, 100)
y = np.exp(x)/(1+np.exp(x))
fig,ax=plt.subplots(figsize=(9,6), dpi=105.3)
ax.axhline(0, color='black', linestyle=":")
ax.axhline(1, color='black', linestyle=":")
ax.axvline(0, color='red', linestyle=":")
ax.plot(x,y)

This is a sigmoid function used in Logistic Regression classification task.

If we have a default classification task, where we classify $Y$ (the outcome) to have values either 0 (No) and 1 (Yes) based on a sigmoid function.

If we predict $\hat Y > 0.5$, this means we predict the Yes answer, else we predicted No answer. The red dotted line is the separator.

We can use for probability notation $Pr(Y=1 \vert X=x)$ a short form $P(X)$.

So we can write:

$P(X) = \Large{\frac{e^{\beta_0+\beta_1X}}{1 + e^{\beta_0+\beta_1X}}}$

Logit trick

Having the form of sigmoid function allows us never to have problems with probability greater than 1 and lower than 0, but how can we get our betas back?

If we use the log odds transformation or logit transformation we get back the linear function: $\beta_0 + \beta_1X$.

$\beta_0 + \beta_1X = log(\frac{P(X)}{1-P(X)})$.

So this is our sigmoid driven model, but how can we estimate the parameters $\beta_0, \beta_1$?

We pick $\beta_0$ and $\beta_1$ to maximize the likelihood of the observed data.

$l(\beta_0, \beta_1)=\displaystyle \prod_{i:y_i=1} p(x_i)\prod_{i:y_i=0} (1-p(x_i))$

In 1922 R. A. Fisher introduced the method of maximum likelihood. He first presented the numerical procedure in 1912.

How to solve LogisticRegression programmatically?

In R you can use the glm function for this, because just a simple linear model works. In scikit-learn use LogisticRegression from sklearn.linear_model and play with the additional parameters.

Coefficient names

Coefficient $\beta_0$ is called the intercept, and $\beta_1$ is called the slope or balance. In scikit-learn these will be intercept_ and coef_ parameters.

Alternative names

Logistic regression is also called logit regression, maximum-entropy classification (MaxEnt) or the log-linear classifier.