Random Processes

Table of Contents:

• Random sample
• Bernoulli trials
• Poisson process
• A renewal process
• Markov process
• Random walks
• Brownian motion

Random sample

A random sample is a sequence of random variables. Random variables should be independent and identically distributed (IID).

Bernoulli trials

Bernoulli trials is random processes. The process consists of:

• two outcomes
• independent trials
• constant probabilities from trial to trial.

Bernoulli random processes is the mathematical abstraction of coin tossing. It is a sequence of independent and identically distributed (iid) random variables (random sample).

Each random variable takes values:

• 1 (with probability $p$)
• 0 (with probability $1-p$)

This process “coins” the following probability distributions:

• binomial
• geometric
• negative binomial

Poisson process

The Poisson process is used to model random “points” in both time and space:

• arrival times
• mouse click times
• customer purchase time
• positions of flaws in material
• counting events in some time interval

These probability distributions came out from Poisson process:

• Poisson
• exponential
• gamma distribution

A renewal process

A renewal process is an idealized stochastic model for “events” that occur randomly in time.

We call them renewals or arrivals.

The times between the successive arrivals are independent and identically distributed (iid).

Renewal processes are often found embedded in other stochastic processes, most notably Markov chains.

Markov process

A Markov process is a random process with the assumption that the future is independent of the past, given the present.

Markov processes are the natural stochastic analogs of the deterministic processes described by differential and difference equations.

A Markov process with a discrete state space is called a Markov chain.

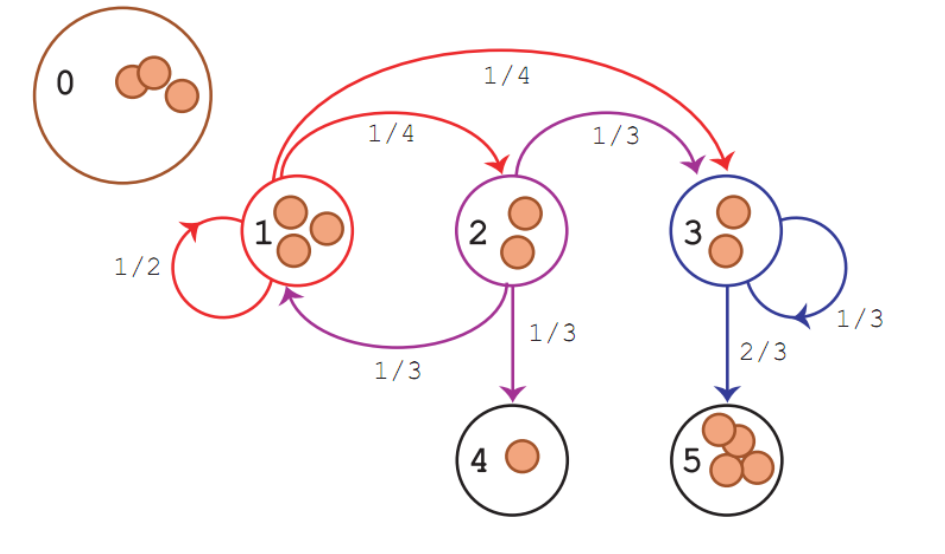Example of Markov Chain

Random walks

Karl Pearson coined the term random walk while solving a problem describing a random walk on the plane.

The simple random walk process is a minor modification of the Bernoulli trials process and it is a discrete time analogue of the Brownian motion process.

${X}$ is called simple random walk with parameter $p$ if:

• ${U} = (U_1, U_2, \ldots)$ is sequence of independent random variables (random sample) taking values from ${-1, 1}$, with probability $p$ and $1-p$ respectively, where $0 \le p \le 1$.

• ${X} = (X_0, X_1, X_2, \ldots)$ is partial sum process associated with $U$ where:

Partial sums are defined as:

$\begin{aligned}X_n = \sum_{i=1}^n U_i, \quad n \in N\end{aligned}$

Brownian motion

Brownian motion is a stochastic process. It is also called the Wiener process also.

Let $X(t)$ is a random variable that depends on $t$ where $t \in [0, \infty)$. We can write simple $X(t) = X_t$

We can describe the process as:

• $X_0 = 0$ with probability 1.

• For $0 \leq s < t \leq T$, the increment: $X_t - X_s \sim \sqrt{t-s} \mathcal{N}(\mu, \sigma^2)$ is normally distributed, where $\mathcal{N}(\mu, \sigma^2)$ denotes the normal distribution.

• $X_t$ has independent increments, which means that if $0 \leq s < t < u < v \leq T$, then $X_t - X_s$ and $X_v - X_u$ are also independent.

import numpy as np
from math import sqrt
from scipy.stats import norm
import matplotlib.pyplot as plt
from matplotlib.pyplot import figure
 
 
def brownian(x0, n, dt, delta, out=None):
 
    x0 = np.asarray(x0)
    # for each element of x0, generate a sample of n numbers from a normal PDF
    r = norm.rvs(size=x0.shape + (n,), scale=delta*sqrt(dt))
    if out is None:
        out = np.empty(r.shape)
    # cumulative sum of the random samples
    np.cumsum(r, axis=-1, out=out)
    out += np.expand_dims(x0, axis=-1)
    return out
 
# brownian delta
delta = 2
# total time
T = 10.0
# number of steps
N = 500
# time step size
dt = T/N
# number of lines
m = 3
# empty array storage
x = np.empty((m,N+1))
x[:, 0] = 50
 
brownian(x[:,0], N, dt, delta, out=x[:,1:])
 
t = np.linspace(0.0, N*dt, N+1)
plt.figure(figsize=(9, 6), dpi=180)
for k in range(m):
    plt.plot(t, x[k])  
 
plt.show()

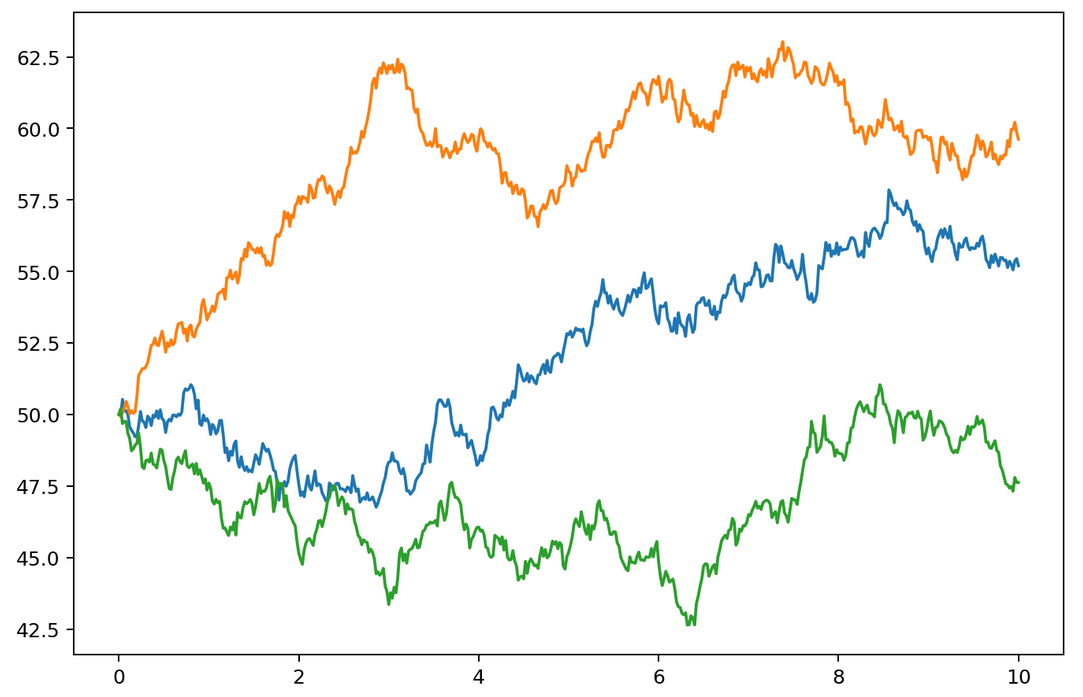Example of Brownian motion