70+ Codility Problems solved in Python

programming review

Table of Contents:

This document has

Iterations

BinaryGap

Returns 100%

def solution(n):
    b=bin(n)[2:]
    s1=False
    tz=0 # temp zeros
    mz=0 # max zeros 
    for e in b:
        if e=='1':
            mz=max(tz,mz)
            tz=0
            s1=True
        else:
            if(s1==True):
                tz+=1
            
            
    return mz

Algorithm 2 returns 100%

def solution(n):
    b=bin(n)[2:] 
    print(b)
    g=0
    j=-1
    j2=-1
    n=-1
    
    for i in range(len(b)):
        #print(i, b[i])
        
        if b[i]=='1' and j>-1 and n>j:
            j2=i            
            g=max(g,j2-j-1)
        
        if b[i]=='1':
            j=i
            
        if b[i]=='0':
            n=i
            
    return g

Algorithm 3 returns 100%

def solution(n):
    # bin representation of N
    b = bin(n)[2:]
    # trim zeros from the right
    b = b.strip("0")
    l = b.split("1")    
    return len(max(l, key=len))

Arrays

CyclicRotation

Scores 100%, check for the len of 0.

def solution(a,k):
    n=len(a)
    if(n==0):
        return []
    k=k%n
    a=a[n-k:]+a[0:n-k]
    return a

OddOccurrencesInArray

Scores 100%, the defaultdict is not needed, simple e in d can do it. Note how we used d.items() to get both keys and values.

def solution(a):
    d = {}
    for e in a:
        if (e in d):
            d[e]+=1
        else:
            d[e]=1
        
    for k,v in d.items():
        if(v%2==1):
            return k

Time Complexity

PermMissingElem

Returns 100%, the key is to sort the array.

def solution(a):
    if (len(a)==0): 
        return 1
    if(max(a) == len(a)):
        return len(a)+1
    
    a.sort() 
    for _ in range(1, len(a)+1):
        if _ != a[_-1]:
            return _

FrogJmp

Scores 100%. We first subtract and then use math.ceil operation.

import math

def solution(x,y,d):    
    r = y-x
    if(r==0): return 0
    
    c = math.ceil(r/d)
    return c

TapeEquilibrium

Solution with 53%

def solution(a):
    m = None # min sum
    l = len(a)  
    
    for p in range(1,l):
        print("p", p)
        ab = abs(sum(a[:p])-sum(a[p:l+1]))
        if (m == None):
            m = ab
        if (m > ab):
            m = ab
            
    return m

Solution with 100%

def solution(a):
    l=len(a)
    ms=None # min sum
    sl=0 # sum left
    sr=sum(a)
    
    for p in range(0,l-1):
        sl=sl+a[p]
        sr=sr-a[p]
        ab=abs(sl-sr)        
        if (ms==None):
            ms=ab
        if (ms>ab):
            ms=ab
    return ms

Counting Elements

FrogRiverOne

This is probable the best task on codility, since it teaches you to use len instead of max.

def solution(x, a):
    l = len(a)  
    s = set() 
    r = -1 # return
    for i,e in enumerate(a):
        s.add(e)     
        if(len(s)==x):
            return i   
    return -1

MaxCounters

Scores 66%

def solution(n, a):
    r = [0]*n
    for v in a:
        if (v==n+1):
            m = max(r)
            r = [m]*n
        else:
            r[v-1] = r[v-1]+1
            
    return r

Scores 100%

from collections import Counter
def maxrep(a):
    if(len(a)==0):
        return 0
    c = Counter(a)
    return c.most_common(1)[0][1]
    
def solution(n, a):
    ll=[[]]# split to multiple lists
    b = 0 # index for the next sublist
    for i in range(0,len(a)):
        if (a[i]== n+1): # break
            b=b+1
            ll.append([])
        else:
            ll[b].append(a[i])

    c = [] # list of max repeat counters
    for l in ll:
        c.append(maxrep(l))

    s = sum(c[:-1])
    r = [s]* n
    if (c[-1]==0):
        return r
    else:
        # get index of last (n+1)
        if(n+1 in a):
            lin = len(a) - a[::-1].index(n+1)
        else:
            lin =0
        
        for v in a[lin:]:
            r[v-1] = r[v-1]+1
        return r

MissingInteger

Scores 100%

def solution(a):
    a = set(a)
    for i in range(1,1000000+1):
        if i not in a:
            return i
    
    return

PermCheck

Scores 100%

# permutation

from random import randint
a = [randint(1, 1000000000) for p in range(0, 100000)]

def missing(a):
    a = set(a)
    for i in range(1,1000000+1):
        if i not in a:
            return i

def solution(a):
    m = max(a)
    if(m!=len(a)):
        return 0
    if(missing(a) <= m ):
        return 0
    return 1

a = [1,3,2,4]
solution(a)

Prefix Sums

PassingCars

Scores 100%. Don’t forget the 1000000000 limit.

def solution(a):
    pc=0
    fz=0
    
    for e in a:
        if pc>1000000000:
            return -1
        if e==0:
            fz+=1
        else:
            pc+=fz           
    
    return pc

GenomicRangeQuery

Scores 100%

def solution(s,p,q):
    n = len(p)
    r = [0]*n
    
    for i in range(n):
        pi=p[i]
        qi=q[i]+1
        ts=s[pi:qi]
        if 'A' in ts:
            r[i]=1
        elif 'C' in ts:
            r[i]=2
        elif 'G' in ts:
            r[i]=3
        elif 'T' in ts:
            r[i]=4
    return r

s,p,q = 'CAGCCTA', [2, 5, 0], [4, 5, 6]
solution(s,p,q)

MinAvgTwoSlice

The standard solution will not perform well so you can get only 50%.

def solution(a):
    n = len(a)
    mi = 0 #index
    tm = max(a) #temp min
    cm = max(a) #current min
    for i in range (0, n):
        for j in range (i+2, n+1):
            tm = sum(a[i:j])/(j-i)
            if tm<cm:
                     cm = tm
                     mi = i
    return mi

The trick is to use ignore slices with more than 3 elements.

def solution(a):
    n = len(a)
    mi = 0 #index
    tm = max(a) #temp min
    cm = max(a) #current min
    for i in range (0, n):
        for j in range (i+2, n+1):
            if(j-i>3): continue
            print(a[i:j])
            tm = sum(a[i:j])/(j-i)
            if tm<cm:
                     cm = tm
                     mi = i
    return mi

However, for loops are slow. This will bring just 60%. The next trick is to avoid for loop.

def solution(a):
    n = len(a)
    mi = 0
    cm = max(a)
 
    for idx in range(0, n-1):
        p = (a[idx] + a[idx+1])/2.0
        if p < cm:
            mi = idx
            cm = p
        if idx < n-2:
            t = (a[idx] + a[idx+1] + a[idx+2])/3.0
            if t < cm:
                mi = idx
                cm = t
 
    return mi

CountDiv

Scores 100%. We first get the first possible value using the // and * trick. If the f is bigger than b, we need to return 0, else we find the distance b-f.

def solution(a, b, k):
    f =  ((a + k -1) // k) * k # first    
    if f > b:
      return 0
 
    return ((b - f) // k) + 1

Sorting

Triangle

Returns 100%

def solution(a):
    n=len(a)
    a.sort()
    for i in range(n-2):
        if a[i]+a[i+1]>a[i+2]:
            return 1
    return 0

Distinct

Returns 100%. Very simple implementation in python.

def solution(a):
    return len(set(a))

Also 100% but with using dictionary.

Example:

def solution(a):
    d=dict()
    for e in a:        
        if e in d:
            d[e]+=1
        else:
            d[e]=1
    #print(d)
    return len(d)

a=[1,1,1,2,2,4,5]
solution(a)

Output:

{1: 3, 2: 2, 4: 1, 5: 1}
4

MaxProductOfThree

Returns 100%

def solution(a):
    a.sort()
    return max(a[0] * a[1] * a[-1], a[-1] * a[-2] * a[-3])

NumberOfDiscIntersections

This solution will bring 56%, and it doesn’t use sorting.

def s(a, i,j):
    if(abs(i-j) <= a[i]+a[j]):
        return True
    else:
        return False

def fc10000000(a):
    s = 0
    for e in a:
        s = s+e
        if s>10000000:
            return True 
    return False
    
    
def solution(a):
    c = 0
    if fc10000000(a):
        return -1
    for i1 in range(0, len(a)):
        for i2 in range(i1+1, len(a)):
            if(s(a, i1, i2)):
                c+=1
                if c>10000000:
                    return -1
    return c

With sorting you can get 100%. Note we cannot use e.sort() in here, instead we sort fist by x[0] and reverse sort by x[1].

def solution(A):
    e = [] # endpoints
    for i, a in enumerate(A):
        e += [(i-a, 1), (i+a, 0)]
    e.sort(key=lambda x: (x[0], not x[1]))
    c=0 # count of intersections
    ac=0 # active circles
 
    for _, start in e:
        if start:
            c+=ac
            ac+= 1
        else:
            ac-= 1
        if c > 10000000:
            return -1 
    return c

Stacks and Queues

Brackets

Recursive brackets. Scores 50%, O(3**N).

def rc(s):
    if (len(s)%2 ==1 ):
        return 0
    if s=='' or s=='()' or s=='[]' or s=='{}':
        return 1
    for _ in range(2, len(s),2):
        if rc(s[0:_])==True and rc(s[_:])==True:
            return 1
    if (s[0]=='{' and s[-1]=='}') or (s[0]=='[' and s[-1]==']') or (s[0]=='(' and s[-1]==')'):
        #print(f"{s[0]}{s[-1]}")
        return rc(s[1:-1])
    return 0

def solution(s):
    return rc(s)

Stack based brackets. Scores 100%.

import random
# s = ''.join([random.choice(['{'*100000, '}'*100000]) for p in range(0, 2)])
#s = '{'*100000 + '}'*100000
#s = '([)()]'

def solution(s):
    if len(s)%2==1: return 0
    st = [] # stack
    pu = ['[', '{', '('] # element to push on stack
    po = {']':'[', '}':'{', ')':'('}
    
    for e in s:
        if e in pu:
            st.append(e) # push
        if e in po.keys():
            if(len(st)==0):
                return 0
            if (st[-1] == po[e]):
                st.pop()
            else:
                return 0
                
    if len(st) == 0:
        return 1
    else:
        return 0

Another solution without using the dict

def solution(a):    
    s = [] # stack
    if a=="":
        return 1
    n = len(a)
    for e in a:        
        if e in ['(', '[', '{']:
            s.append(e)
        else:
            if(len(s)==0):
                return 0
            
            if e == ')' and s[-1] == '(':
                s.pop()
                continue
                
            if e == ']' and s[-1] == '[':
                s.pop()
                continue
                
            if e == '}' and s[-1] == '{':
                s.pop()
                continue
            
    if len(s)==0:
        return 1
    else:
        return 0

Nesting

Same as Brackets task. See Brackets.

StoneWall

Recursive StoneWall scores: 71, O(N**2)

a = [8, 8, 5, 7, 9, 8, 7, 4, 8]
def rec(a):
    if(len(a)==0 or (len(a)==1 and a[0]==0)):
        return 0
    if(len(a)==1):
        return 1
    stones = 0
    m = min(a) # min
    if m>0:
        a = [e-m for e in a]
        stones+=1
    izr = a.index(0)
    stones = stones + rec(a[:izr]) + rec(a[izr+1:])
    return stones  

def solution(a):
    r = rec(a)
    return r
    
solution(a)

This solution scores 100%

def lss(s): # last el of stack
    if len(s)>0:
        return s[-1]
    else: 
        return 0
        
def solution(a):
    n=len(a)
    s=[]#stack    
    cnt=0    
    for e in a:
        if e>lss(s):
            s.append(e)
        elif e==lss(s):
            continue
        else: # e<lss(s)
            while lss(s)!=0 and lss(s)>e:
                s.pop()
                cnt+=1
            if(e!=lss(s)):
                s.append(e)
            
    cnt+=len(s)
    return cnt

We always deal with stones >0. If new element is bigger than the last on the stack, then add that to the stack, if it is a same size do nothing and process the next element of the array of stones.

If the new element is smaller, then every time we pop we increase the counter, and repeat that for all stack. If we get to the same stone size in the stack with the new stone size, we should not pop nor update the counter cnt.

If the stone size is different than what is on stack, just append the stack.

Fish

Scores 87%, directly updating a and b.

from random import randint
def solution(a,b):
    i = 0 # index
    while(len(a)>i+1):
        if (b[i] > b[i+1]): # opposite direction
            if a[i]> a[i+1]:
                a.pop(i+1)
                b.pop(i+1)
            else:
                a.pop(i)
                b.pop(i)
                i=i-1
        else:
            i=i+1

    return len(a)
    
a,b = [randint(-10000, 10000) for p in range(0, 100000)], [randint(0, 1) for p in range(0, 100000)]  
#a,b = [4, 3, 2, 1, 5], [0, 1, 1, 0, 0]
solution(a,b)

Scores 100% with single stack.

def solution(a, b):
    l = 0 # left
    s = [] # stack
    for i in range(len(a)):
        if b[i]==1: # fish moving upwards
            s.append(a[i]) # to the stack
        else: # eat fish mowing downwards.
            while len(s)>0:
                if s[-1]<a[i]:
                    s.pop() # eat from the stack
                else:
                    break
            else:
                l+=1
    l+=len(s)
    return l

Leader

Dominator

Scores 83%

from collections import Counter

def solution(a):
    l = len(a)
    if (l==0): 
        return -1

    c = Counter(a)    
    d = c.most_common(1)[0][1] # dominator
    e = c.most_common(1)[0][0] # element
    if (d<=l//2):
        # not dominator
        return -1
    else:
        # d is dominator
        if (e in a):
            return a.index(e)

Scores 100%

from collections import defaultdict

def solution(a):
    n = len(a)
    if n==0: return -1

    d=defaultdict(lambda: 0)
    dm = a[0] # dominator
    for e in a:
        d[e]+=1        
        if d[dm]<d[e]:
            dm = e
    if(d[dm]> n//2):
        return a.index(dm)
    else:
        return -1

EquiLeader

66% with O(n**2) is the best we can get with calling leader inside for loop. We also have the function that check the leader for the whole array at first, since if there is no leader for the whole array, then we cannot have equileader.

def leader(a):
    n=len(a)
    if (n==0):
        return None
    if (n==1):
        return a[0]
    if (n==2 and a[0]==a[1]):
        return a[0]
    
    d=sorted(a)[n//2]
    
    dn=0
    for e in a:
        if e==d:
            dn+=1 
    
    if dn > n//2:
        return d
    else:
        return None
def solution(a):
    n = len(a)
    l = leader(a)
   
    if None==l:
        return 0
    if 1==n:
        return 0
    if 2==n:
        return 1
    cnt=0
    for i in range(0, n-1):
        l1 = a[:i+1]
        l2 = a[i+1:]
             
        l1v = leader(l1)
        l2v = leader(l2)
        if (l1v == l2v and l1v!=None):
            cnt+=1
    return cnt

The provided example would create lists like this:

[4] [3, 4, 4, 4, 2]
[4, 3] [4, 4, 4, 2]
[4, 3, 4] [4, 4, 2]
[4, 3, 4, 4] [4, 2]
[4, 3, 4, 4, 4] [2]

and check as separate. The improvident would be to not to call leader checker inside the loop for each list.

The next solution scores 100%.

def leader(a):
    n=len(a)
    if (n==0):
        return None
    if (n==1):
        return a[0]
    if (n==2 and a[0]==a[1]): 
        return a[0]

    d=sorted(a)[n//2]
    dn=0
    for e in a:
        if e==d:
            dn+=1 
    if dn > n//2:
        return d
    else:
        return None
    
def solution(a):
    n = len(a)
    l = leader(a)
   
    if None==l:
        return 0
    if 1==n:
        return 0
    if 2==n:
        return 1
    
    cnt=0
  
    dl,dr = {},{}
    for i in range(n): #init dr
        if a[i] not in dr:
            dr[a[i]]=1
        else:
            dr[a[i]]+= 1
    ld = a[0] # leader

    for i in range(n): 
        if a[i] not in dl:
            dl[a[i]]=1
        else:
            dl[a[i]]+=1

        dr[a[i]]-=1

        if dl[ld] < dl[a[i]]:
            ld = a[i] # new leader from dl

        if (i+1) // 2 < dl[ld] and (n - (i+1)) // 2 < dr[ld]:
            cnt += 1
    return cnt

Note we don’t have to sort dictionary elements, because the first list dl at the very start has 1 element as leader. Later we check every next element if it has greater value than that leader.

We also don’t need to check the the leader for the second dictionary, so no need for this code:

print(max(dl, key=dl.get))
print(dl)
print(max(dr, key=dr.get))
print(dr)
print('ld', ld)
print('~~~')

because we increase the counter just based on the fact that the same leader for both the dicts has more than half elements.

Another important thing is to check at the very start if the list we got as input has the leader. Without that we will loose some percentage.

Note it is not needed to sort the dictionary also:

print(sorted(dr.items(), key=lambda x: x[1], reverse=True ))

Slightly more elegant solution would be to use defaultdict from collections, also scores 100%.

from collections import defaultdict

def leader(a):
    n=len(a)   
    if (n==0): 
        return None
    if (n==1): 
        return a[0]
    if (n==2 and a[0]==a[1]): 
        return a[0]    
    
    d=sorted(a)[n//2]
    
    dn=0
    for e in a:
        if e==d:
            dn+=1 
    
    if dn > n//2:
        return d
    else:
        return None    
    
def solution(a):
    n = len(a)
    l = leader(a)
   
    if None==l:
        return 0
    if 1==n:
        return 0
    if 2==n:
        return 1
    
    cnt=0  
    dl,dr = defaultdict(lambda : 0),defaultdict(lambda : 0)
    
    
    for i in range(n): #init dr
        dr[a[i]]+= 1

    ld = a[0] # leader
    for i in range(n): 
        dl[a[i]]+=1
        dr[a[i]]-=1
        
        if dl[ld] < dl[a[i]]:
            ld = a[i] # new leader from dl
            
           
        if (i+1) // 2 < dl[ld] and (n - (i+1)) // 2 < dr[ld]:
            cnt += 1
    return cnt

Maximum Slice Problem

MaxProfit

Using just three temp variables.

def solution(a):
    smax=None
    smin=None
    mp=0 # max profit
    
    for e in a:
        if smin==None:
            smin=e
        if smax==None:
            smax=e
        
        if e > smax:
            smax=e
        if e < smin:
            smin=e
            smax=e
        
        if mp < smax-smin:
            mp = smax-smin
            
    return mp

Another solution jump Scores 100%. In here we have an array of prices at particular day such as this one a = [5,4,3,2,3,4,5,6,5,4,5,6,7,1] and we would like to find the maximum jump mj or maximum profit we may get.

Local jump lj is non negative local jumps, and sj is single jumps sj may be negative.

from random import randint
# a = [5,4,3,2,3,4,5,6,5,4,5,6,7,1]
a = [randint(0, 200000) for p in range(0, 400000)]
def jump(a):
    lj, mj = 0,0
    n = len(a)
    for i in range(0, n-1):
        sj = a[i+1]-a[i]
        if sj<=0:
            lj=max(0, lj+sj)
        else:
            lj=lj+sj
            mj = max(mj,lj) # max jump
    return mj

jump(a)

General case max profit:

# max profit with k transactions
def solution(a,k):
    n=len(a)
    if n==0:
        return 0
    # profits   
    p = [[0 for d in a] for t in range(k+1)] 
    print(p)

    for t in range(1,k+1):
        m = float("-inf")
        for d in range(1, len(a)): 
            m=max(m,p[t-1][d-1]-a[d-1]) 
            print(m)
            p[t][d]=max(p[t][d-1],m+a[d]) 
    
    print(p)
    return p[-1][-1]

MaxSliceSum

Scores 100%. This problem should search in array to find the slice with max sum.

m and ms do represent local and final max sum. For instance:

a=[3, 2, -6, 4, 0] # array
m=[3, 5, -1, 3, 3] # local max sum

ms is maximum of m but we don’t keep m as an array more like a running variable.

a=[3, 2, -6, 4, 0]
def solution(a):    
    m,ms=a[0],a[0]
    for i in range(1, len(a)):
        m=max(a[i], m+a[i])
        ms=max(m,ms)
    return ms
solution(a)

MaxDoubleSliceSum

Another problem from codility

Scores 100%

a=[3,2,6,-1, 4, 5, -1, 2]
def solution(a):
    n = len(a)
    k1=[0]*n
    k2=[0]*n
    for i in range (1, n):
        k1[i] = max(k1[i-1] + a[i], 0)
    for i in range (n-2, 0, -1):
        k2[i] = max(k2[i+1] + a[i], 0)
    m=0 # max
    for i in range(1, n-1):
        m = max(m, k1[i-1]+k2[i+1])
    return m

solution(a)

Prime and composite numbers

MinPerimeterRectangle

def solution(n):
    i=1
    d=0
    f=[]
    while(i*i<n):
        if n%i==0:
            f.append(i)
            f.append(n//i)
        i+=1
    if(i*i==n):
        f.append(i)
        return 2*(i+i)
    else:
        return 2*(f[-1]+f[-2])

CountFactors

Peaks

def alf(n):
    i=2
    t = n
    f=[]
    while(t>1):
        if t%i==0:
            f.append(i)
            t = t/i
        else:
            i+=1
    
    return f

def fp(a):
    n = len(a)
    p = [0]*n
    for i in range (1,n-1):
        if a[i-1] < a[i] and a[i]>a[i+1]:
            p[i]=1
    return p
    
def has1(p,d):
    ret=False 
    n = len(p)
    zones=[0]*d
    for i in range (0, n):
        zone = i//(n//d)
        if p[i]==1:
            zones[zone]=1
    if min(zones)==1:
        ret = True
    return ret


def solution(a):
    p = fp(a)
    n = len(a)
    f = list(alf(n))[::-1]
    for i in f:
        if has1(p,i):
            return i

Flags

Returns 100%

a=[1, 5, 3, 4, 3, 4, 1, 2, 3, 4, 6, 2]

def fp(a):
    n = len(a)
    p = [0]*n
    for i in range (1,n-1):
        if a[i-1] < a[i] and a[i]>a[i+1]:
            p[i]=1
    return p

def ck(a,x):
    n = len(a)    
    f=x
    pos=0    
    while f>0 and pos<n:
        if a[pos]==1:
            f-=1
            pos+=x
        else:
            pos+=1
    return f==0    

def solution(a):
    p = fp(a)
    mf = 0
    i = 1
    while ck(p,i):
        i*=2
    print(i)
    
    for j in range (i, 0, -1):
        if (ck(p,j)):
            mf = j
            break
    return mf

Sieve or Eratosthenes

CountSemiprimes

Scores 55%

n,p,q = 26, [1, 4, 16], [26, 10, 20]

def semi_primes(N):    
    s = set()
    m = [1]* (N+1) # mask
    m[0] = m[1] = 0
 
    i = 2
    while (i*i <= N):
        if m[i] == 1:
            for j in range(i*i, N+1, i):
                m[j] = 0
        i += 1
 
    i = 2    

    while (i*i <= N):
            if m[i] == True:
                for j in range(i*i, N+1, i):
                    if (j % i == 0 and m[j//i] == True):
                        s.add(j)
            i += 1

    return s


def solution(n,p,q):
    sp = semi_primes(n)
    r=[0]*len(p)
    for i in range(0,len(p)):
        print(q[i],p[i])
        r[i] =len([e for e in sp if e>=p[i] and e<=q[i]])
        
    return r

solution(n,p,q)

CountNonDivisible

Scores 55%

def cnt(n, a):
    r=0
    for e in a:
        if n%e==0:
            r+=1
    return r

def solution(a):    
    n = len(a)
    ra=[0]*n   
    for i in range (0,n):
        ra[i]=n-cnt(a[i],a)
        
        
    return ra

Euclidean Algorithm

ChocolatesByNumbers

Scores 100%

def gcdm(a, b):
    if a % b == 0:
        return b
    else:
        return gcdm(b, a % b)

def solution(n, m):
    m = m%n
    if(m==0):
        return 1
    else:
        return int(n/gcdm(n,m))

CommonPrimeDivisors

Scored 84%

def alf(n):
    i=2
    t = n
    f=[]
    while(t>1):
        if t%i==0:
            f.append(i)
            t = t/i
        else:
            i+=1
    
    return f

def solution(a,b):
    h=0 # how many

    # prepare d
    d ={}
    s = set(a+b)
    for e in s:
        d[e]=set(alf(e))
    
    
    for i in range(0,len(a)):
        if d[a[i]] == d[b[i]]:
            h+=1
    return h
    
    
a = [15,10,3]
b = [75, 30,5]
solution(a,b)

Fibonacci Numbers

FibFrog


This solution will get 83%

def fib(n=50):
    # there are 26 numbers smaller than 100k
    f = [0] * (n)    
    f[1] = 1
    for i in range(2, n):
        f[i] = f[i - 1] + f[i - 2]
    return f

def solution(a):
    a.insert(0, 1)
    a.append(1)
    n=len(a)
    steps = [0]+[n]*(n-1)
    
    for p in range(1, len(steps)): # position
        s_min = n
        for jump in fib():
            prev_leaf = p - jump
            if prev_leaf >= 0:
                if a[prev_leaf] == 1 and steps[prev_leaf] + 1 < s_min:
                    s_min = steps[prev_leaf] + 1
            else:
                break
        steps[p] = s_min
    
    return steps[-1] if steps[-1] != n else -1

Ladder

def fib(n=50):
    # there are 26 numbers smaller than 100k
    f = [0] * (n)    
    f[1] = 1
    for i in range(2, n):
        f[i] = f[i - 1] + f[i - 2]
        
    return f
        
f = fib(n=50)[1:]


def step2(n=30):
    s = [0]*n
    for i in range(1, n):
        s[i]=2**i    
    return s

s = step2()

def solution(a,b):
    n = len(a)
    r = [0]*n
    for i in range(0,n):
        r[i]=f[a[i]]%s[b[i]]
    return r

MinMaxDivision

I took the solution from Martin’s blog. We know that max(a) is the minimum value we can achieve, at the same time the sum(a) is the max value, so the value we search form must be in between. We use // operation to evaluate the new value.

This returns 100%:

def chk(a, c, s):
    ts = 0 # temp sum
    tc = 0 # temp cnt
 
    for e in a:
        if ts + e > s:
            ts = e
            tc += 1
        else:
            ts += e
        if tc >= c:
            return False

    return True
 
def bs(a, m):
    n=len(a)
    l = max(a) # smallest value
    u = sum(a) # max value

    if m == 1: return u
    if m >= n: return l

    while l <= u:
        nv=(l+u)//2 # new value
        if chk(a, m, nv):
            u=nv-1
        else:
            l=nv+1
 
    return l
 
def solution(k,m,a):
    return bs(a,k) # binary search

This solution doesn’t tell you anything on grouping but based on the information we achieve, we can create the grouping later.

NailingPlanks

This solution will return 50% with 100% correct approach.

def solution (a,b,c):
    n=len(a)
    ab=list((zip(a,b)))
    m=dict() #[0]*n
    
    for i,e in enumerate(c):
         for j,f in enumerate(ab):
            if f[0]<=e<=f[1]:
                m[j]=1
                #print(i, e, j, f[0], f[1], len(m), m)
                if len(m)==n:
                    return i+1
    return -1

For the performance improvement check Martin’s blog and even further improvements Dragan’s blog.

Caterpillar method

AbsDistinct

Returns 100%

def solution(a):
    a = [abs(i) for i in a]
    return len(set(a))

You can also use map function

def solution(a):
    return len(set(map(abs,a)))

CountDistinctSlices

This solution will get you 70%


def solution(m,a):   
    n = len(a)    
    m = max(a)
    c=0 #counter
    for i in range(0,n):
        j=i
        while len(set(a[i:j+1]))==j-i+1: 
            c+=1
            j=j+1
    return c

This will get 100%

def solution(m, a):
    n = len(a)
    m = max(a)
    c = 0
    mask = [0]*(m+1)
    
    l,r=0,0 # left and right slice indices    
    while (l<=r< n):
        while (r < n and mask[a[r]] != 1):
            c += (r-l+1)
            mask[a[r]] = 1
            r += 1
            print(l,r,mask, c)
        else:
            while r < n and l < n and a[l] != a[r]:
                mask[a[l]] = 0
                l += 1
            mask[a[l]] = 0
            l += 1
            print(l,r,mask, c)
    return min(c, 1000000000) 

a =[3, 4, 5, 5, 2]
solution(5,a)
l r mask c
0 1 [0, 0, 0, 1, 0, 0] 1
0 2 [0, 0, 0, 1, 1, 0] 3
0 3 [0, 0, 0, 1, 1, 1] 6
3 3 [0, 0, 0, 0, 0, 0] 6
3 4 [0, 0, 0, 0, 0, 1] 7
3 5 [0, 0, 1, 0, 0, 1] 9
4 5 [0, 0, 1, 0, 0, 0] 9

CountTriangles

Next solution returns 63%, it is 100% correct but not fast.

def solution(a):
    n=len(a)
    if n<3:
        return 0
    
    a.sort()
    c=0 # counter
    for i in range(0, n-2):
        for j in range(i+1, n-1):
            for k in range( j+1, n):
                if a[i]+a[j]>a[k] and a[j]+a[k]>a[i] and a[k]+a[i]>a[j]:
                    c+=1
                else:
                    continue
    return c

This is 100% solution:

def solution(a):
    n=len(a)
    a.sort()
    c=0
    for p in range(0, n-2):
        q=p+1
        r=p+2
        while r<n:
            if a[p]+a[q]>a[r]:
                c+=r-q
                r+=1
            elif q<r-1:
                q+=1
            else:
                r+=1
                q+=1
    return c

MinAbsSumOfTwo

This solution is 100% but it is slow so you will get 36% overall.

def solution(a):
    n=len(a)
    if n==1:
        return abs(a[0]+a[0])
    m = 2000000000
    for i in range(n):
        for j in range(n):
            m=min(m,abs(a[i]+a[j]))
    return m

The improvement is to sort the array and use caterpillars. This solution will bring 100%. We sort the array and start with from array top-left and top-right positions. If the sum of two elements from these positions is >0 then we move the right index to the left, this should make the sum smaller. Case the sum is negative, we increase the left index, this should make the sum bigger, or close to 0.

def solution(a):
    n=len(a)
    
    if n==1:
        return abs(a[0]+a[0])

    a.sort()
    #print(a)
    
    l=0 # first
    r=n-1 # last 
    m = 2000000000

    while l<=r:
        dif= a[l]+a[r] 
        
        #print('dif:', dif, 'a[l]:', a[l], 'a[r]:', a[r],'l:', l, 'r:', r)
        if dif==0:
            return 0
        
        m = min(m,abs(dif))
        if dif>0:
            r=r-1
        else:
            l=l+1

    return m

Greedy algorithms

TieRopes

Scores 100%

def solution(k,a):
    an = [e if e<k else 0 for e in a]
    gek = 0
    for e in an:
        if e==0:
            gek+=1

    ts=0
    for e in an:
        if e==0:
            ts=0
        else:
            ts+=e
            if ts>=k:
                gek+=1
                ts=0
    return gek

MaxNonoverlappingSegments

This solution scores 60%.

We create list c of segment sizes. The idea is to add the minimum length sizes first, because this will make more room for the other segments. If we would add the biggest segment first, this will not be smart. We also have the dict d where we check what has been left.

Function tta is try to add segment t to dict d if possible then return 1 if you add else 0 if you cannot add. Adding a segment t is based on values form the segment start and end.

def tta(d, t):
    _,a,b = t
    none=True
    for i in range(a,b+1):
        if d[i]==1:
            none=False
            
    if none==True:
        for i in range(a,b+1):
            d[i]=1
        return 1
    else:
        return 0

def solution(a,b):
    n=len(a)
    if n==0:
        return 0
    c=[]
    for i in range(n):
        c.append(b[i]-a[i])
    
    d = dict(zip([i for i in range(min(a), max(b)+1)], iter(lambda:0,1)))
    s = sorted(zip(c,a,b)) # array of sorted segments
    
    cnt =0
    for c,a,b in sorted(zip(c,a,b)):
        cnt+=tta(d,(c,a,b))
    return cnt

This algorithm is not 100% correct, even though it scores 100% for correctness. We can see that from one example from the performance tests, got 26 expected 27. This is because, even though we add segments sorted by size, and then by end…

sorted(zip(c,a,b))
# is equivalent to because originals was already sorted by end
sorted(zip(c,a,b), key=lambda _:(_[0], _[2]))

better would be to deal segments as presented (sorted by end); not even sorted by size. Since this problem requires greedy algorithm, let’s provide one.

def solution(a,b):
    n=len(a)
    if n==0:
        return 0
     
    cnt=1
    e = b[0]
    for i in range(1, n):
        if a[i]>e:
            cnt+=1
            e=b[i]

    return cnt

We count the first segment and traverse all the segments marking the end e each time. We use that end e to check if our new segment can fit.

Dynamic Programming

NumberSolitaire

This solution is not perfect but it will bring 50%.

'find smart index'
def max6(a,i,j):
    n=len(a)
    
    for k in range (i,min(n,j+1)):
        if a[k]>=0:
            return k
    
    if i<=n and j>=n:
        return n-1
    
    ima=i    
    for k in range (i,j+1):
        if a[k]>=a[ima]:
            ima=k
    return ima

a=[-1, -2, -3, -4, -5, -1, -1, -1, -2, -3, -4, -5, -1, -1, -1, -2, -3, -4, -5, -1, -1]
i=[ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]
a=[1, -2, 0, 9, -1, -2]
i=[0,  1, 2, 3,  4,  5]
def solution(a):
    n=len(a)
    s=a[0]
    ind=0
    
    while ind!=n-1:
        ind = max6(a, ind+1, ind+6)
        print(':', len(a), ind+1, ind+6)
        print('ind',ind)
        s=s+a[ind]
        
    return s

solution(a)

You can track arrays a and index i down below. How it works? If it is a positive number or 0 we take this number and increase the sum. If it is all negative numbers in the slice of 6 numbers, we take the last max, no matter where it is placed. This may lead to non optimal solutions, but it scores 50%.

Perfect score of 100% if we use dynamic programming. We calculate a map that holds the max values.

def solution(a):
    n=len(a)    
    m = [a[0]]*(n + 6) # map
    # print(m)
    for i in range(1, n):
        m[i+6] = max(m[i:i+6])+a[i]
        #print ('i:',i, 'a[i]', a[i] , ' m[6:]', m[6:])
    return m[-1]

m[i:i+6] is array slice meaning last 6 values of the map. m is a map that we calculate dynamically.

For example if we have a=[1, -1, -2, -3, -4, -5, -6, 2] there is how the map is progressing.

[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
i: 1 a[i] -1  m[6:] [1, 0, 1, 1, 1, 1, 1, 1]
i: 2 a[i] -2  m[6:] [1, 0, -1, 1, 1, 1, 1, 1]
i: 3 a[i] -3  m[6:] [1, 0, -1, -2, 1, 1, 1, 1]
i: 4 a[i] -4  m[6:] [1, 0, -1, -2, -3, 1, 1, 1]
i: 5 a[i] -5  m[6:] [1, 0, -1, -2, -3, -4, 1, 1]
i: 6 a[i] -6  m[6:] [1, 0, -1, -2, -3, -4, -5, 1]
i: 7 a[i] 2  m[6:] [1, 0, -1, -2, -3, -4, -5, 2]

MinAbsSum

With the simplest possible solution you will get 27% already.

def solution(a):
    n=len(a)
    ms=0
    for i in range (0,n):
        if ms>0:
            s=-1
        else:
            s=1
        if a[i]<0:
            s=-s
        ms+=s*a[i]
    return abs(ms)

To solve it in golden way you will get 100%

Challenges

Buckets

Returns 100%

def solution(n, q, b, c):
    if q==1:
        return 0
    
    dd={} # dict of dicts
    for i in range (n):
        dd[i]={}
    
    for i in range (len(b)):        
        if not c[i] in dd[b[i]]:
            dd[b[i]][c[i]]=1
        else:
            dd[b[i]][c[i]]+=1
            if dd[b[i]][c[i]]==q:
                return i
    return -1

SheepAndSunshades

This will get you 50% with 100% correct answer. In here you fist define the mp function which is the difference between two points.

def mp(p1,p2):
    return max(abs(p1[0]-p2[0]), abs(p1[1]-p2[1]))

def solution(a,b):
    n=len(a)
    m = 1000000
    for i in range(n-1):
        for j in range(i+1,n):
            p1=a[i],b[i] 
            p2=a[j],b[j] 
            m = min(m,mp(p1,p2))
    return m//2

But how to make it even faster? This will return 85%, but in fact should be 100%.

def mp(p1,p2):
    return max(abs(p1[0]-p2[0]), abs(p1[1]-p2[1]))
    
def solution(a,b):
    n=len(a)
    z = sorted(zip(a,b))
        
    m=1000000
    for i in range(n-1):
        p1=z[i][0],z[i][1]
        p2=z[i+1][0],z[i+1][1]
        m = min(m,mp(p1,p2))
    
    z = sorted(zip(b,a))
    for i in range(n-1):
        p1=z[i][0],z[i][1]
        p2=z[i+1][0],z[i+1][1]
        m = min(m,mp(p1,p2))

    return m//2

Rivers

def gun(i,j,a,v): # get unvisited neighbors
    n=[] 
    if i>0 and not v[i-1][j]:
        n.append([i-1,j])
                 
    if i<len(a)-1 and not v[i+1][j]:
        n.append([i+1,j])
                 
    if j>0 and not v[i][j-1]:
        n.append([i,j-1])         
   
    if j<len(a[0])-1 and not v[i][j+1]:
        n.append([i,j+1])
                 
    return n

def cel(i,j, a,v,s): # check every cell    
    
    c = 0 # river size counter
    ns=[[i,j]] # node stack contains single river

    while len(ns):
        cn = ns.pop() # current node
        i,j=cn[0],cn[1]
        #print(ns)        
        
        if v[i][j]:
            continue
            
        v[i][j]=True
        
        if a[i][j]==0:
            continue
            
        c+=1

        un = gun(i,j,a,v) # get unv. n.
        for n in un:
            ns.append(n)
            
    if c>0:
        s.append(c)

    

def solution(a):    
    s=[] # sizes
    v=[[ False for r in a] for c in a[0] ]# visited

    for i in range(len(a)):
        for j in range(len(a[0])):            
            cel(i,j, a,v,s) # check every cel

    return s

a=[[1,0,0,1,0],[1,0,1,0,0],[0,0,1,0,1],[1,0,1,0,1],[1,0,1,1,0]]
r=solution(a)
print(r)

DifferentCharacters

def solution(s,k):
    n=len(s)   
    d=dict()
    ds=dict()# start position
    de=dict() # end position
    for i in range(n):
            if not s[i] in ds:
                ds[s[i]]=i
            if not s[n-1-i] in de:
                de[s[n-1-i]]=n-1-i
    for e in s:        
        if not e in d:
            d[e]=1            
        else:
            d[e]+=1
    ne = len(d)    
    dd=dict() # diff
    for e in de:
        dd[e]=de[e]-ds[e]
    
    r=0
    if k>=ne:
        return -1
    else:
        r=ne-k    
    
    ltr = sorted(dd.items(), key=lambda x: x[1] )[:r]
    
    minmin, maxmax= n,0
    for e in ltr:
        minmin=min(minmin, ds[e[0]])
        maxmax=max(maxmax, de[e[0]])
        
    su = 1+ maxmax-minmin
    
    if su==n:
        return -1
    return su

DreamTeam

Returns 100%:

def solution (a,b,f):
    n=len(a)
   
    c=[0]*n
    for i in range (n):
        c[i] = a[i]-b[i] 
   
    sz = sorted(zip(c,a,b), reverse=True)
   
    s=0    
    for tri in sz:
        if f>0:
            s+=tri[1]
            f-=1
        else:
            s+=tri[2]
    return s

MaxPathFromTheLeftTopCorner

Scores 77%

def re(a, i,j): # recursive function on point (i,j)
    rn = len(a)
    cn = len(a[0])
    
    # if we must go right
    if j+1 >= cn and i+1 < rn:
        return str(a[i][j]) + re(a,i+1,j)
    
    # if we must go down
    if j+1 < cn and i+1 >= rn:
        return str(a[i][j]) + re(a,i,j+1)
    
    # if we can go either way
    if j+1 < cn and i+1 < rn:
        
        # if both options have the same value
        if a[i][j+1] == a[i+1][j]:
            return str(a[i][j]) + max(re(a,i+1,j),re(a,i,j+1))
        
        if a[i][j+1] > a[i+1][j]: # bigger is to the right
            return str(a[i][j]) + re(a,i,j+1)            
        else: # bigger is to down
            return str(a[i][j]) +re(a,i+1,j)
        
    if i==rn-1 and j== cn-1:
        return str(a[i][j])


def solution(a):
    rn = len(a)
    cn = len(a[0])
    r = re(a, 0,0)
    return r

FloodDepth

Scores 100%

import operator
def peaks2(a):
    n=len(a)
    p=[0]*n #peaks
    if a[0]>a[1]:
        p[0]=1 # peak
    if a[-1]>a[-2]:
        p[-1]=1 # peak
        
    for i in range (1,n-1):
        if a[i-1]<a[i]>a[i+1]:
            p[i]=1
        if a[i-1] < a[i] and a[i]==a[i+1]:
            p[i]=1 #also peak
        if a[i-1] == a[i] and a[i]>a[i+1]:
            p[i]=1 # also peak
            
    return p
    
def solution(a):    
    n=len(a) 
    if n<2:
        return 0
    p2=peaks2(a)
    p=list(map(operator.mul, p2,a))
    np=[0]*n # new value
    lv=0

    for i in range (0,n):
        if p[i]>1 and p[i]>lv:
            lv= p[i]
            np[i]=p[i]
    lv=0
    for i in range (n-1, -1, -1):
        if p[i]>1 and p[i]>lv:
            lv= p[i]
            np[i]=p[i]

    wd=[0]*n # water level
    s=[np[i] for i in range(0,n) if np[i]>0 ]

    for i in range(0, len(s)-1):
        s[i]=min(s[i],s[i+1])

    j=-1
    for i in range (0,n):
        if np[i]>1:
            j+=1
        elif j<len(s)-1 and j!=-1:
                wd[i]=s[j]

    m=0 # max flood deep
    for i in range (0,n):
        if wd[i]>0:
            m=max(m,wd[i]-a[i])
    return m

We first calculate the peaks.

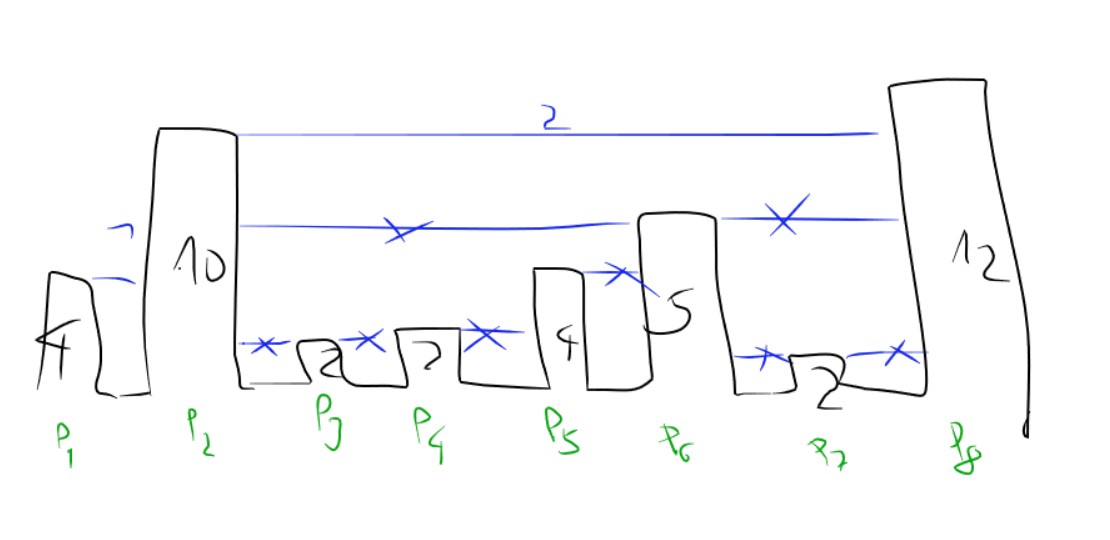
peaks

But then from these calculated peaks only some will be important to hold the level of the water. To find them we go from left to right finding increasing and from right to left finding increasing peaks. All other peaks will be removed.

Once we have the valid peaks the water level will be min(p1, p2) between two valid peaks.

We may not use import operator trick if we update the peaks2 function to return real values instead one and zero.

MaxZeroProduct

This is 100% correct solution but with TIMEOUT ERROR, and this all brings 55% result.

def hmz(s): # how many zeros
    s=str(s)
    n=len(s)
    c=0
    for i in range(n-1, -1, -1):
        if s[i]=='0':
            c+=1
        else:
            break
    return c

def solution(a):
    n=len(a)
    if n<2:
        return 0
    d=dict()
    for i in range(n-2):
        for j in range (i+1, n-1):
            for k in range(j+1, n):
                d[i,j,k]=a[i]*a[j]*a[k]
    m=0
    for v in d.values():
        m=max(m,hmz(v))
    return m

TheaterTickets

This is 100% correct but 58% at the end. Not performing fast.

def solution(a):
    n=len(a)
    if n<2:
        return 0
    d=dict()
    for i in range(n-2):
        for j in range (i+1, n-1):
            for k in range(j+1, n):
                d[i,j,k]=(a[i],a[j],a[k])
    #print(d)
    
    s = set(d.values())
    #print(s)
    return len(s)

Canoeist

from collections import deque

def solution(a,k):
    n=len(a)
    s=deque()
    f=deque()
    for i in range(n-1):
        if a[i]+ a[-1]<=k:
            s.append(a[i])
        else:
            f.append(a[i])    
    f.append(a[-1])   
    
    c=0
    while s or f:
        if len(s)>0:
            s.pop()
        f.pop()        
        c+=1        
        if (not f and s):
            f.append(s.pop())
        while(len(f) > 1 and f[-1] + f[0] <=k):
            s.append(f.popleft())
    return c

BeautifulPassword

100% correct but scores 50% overall

def chk(l):
    for e in l:
        if e%2==1:
            return False
    return True

def solution(s):
    n=len(s)
    
    from collections import Counter
    c = Counter(s)
    m=0 # max
    
    for i in range(n-1):
        for j in range(i+1,n):
            c=Counter(s[i:j+1])
            l=list(c.values())
            if chk(l)==True:
                m=max(m,sum(l))
    return m

PascalTriangles

This solution is 100% correct but 50% is the final result because it is not performing fast.

def solution(a):
    
    s=0    
    a=[int(e) for e in a]
    s=sum(a)
    
    while(len(a)>1):
        a=[a[i] or a[i+1] for i in range(len(a)-1)]
        s+=sum(a)    
    
    return s

This would bring 100%

def sumg(n):
    return int(n*(n+1)/2)

def solution(a):
    m=1000000000
    b=''.join(['1' if e==True else '0' for e in a ])    
    n=len(a)    
    s=sumg(n)
    l=b.split('1')
    for e in l:
        if len(e)>0:
            s-=sumg(len(e))
            
    if s>m:
        return m
    else:
        return s

CoverBuildings

50% and 100% correct

import operator
def peaks2(a):
    n=len(a)
    p=[0]*n #peaks
    if a[0]>a[1]:
        p[0]=1 # peak
    if a[-1]>a[-2]:
        p[-1]=1 # peak
        
    for i in range (1,n-1):
        if a[i-1]<a[i]>a[i+1]:
            p[i]=1
        if a[i-1] < a[i] and a[i]==a[i+1]:
            p[i]=1 #also peak
        if a[i-1] == a[i] and a[i]>a[i+1]:
            p[i]=1 # also peak
            
    return p
def solution(a):
    n=len(a)
    if n==1:
        return a[0]
    
    p2=peaks2(a)
    p=list(map(operator.mul, p2,a))
    print(p)

    m=max(a)
    
    # max index
    mis=[i for i in range(n) if a[i] in p and a[i] > 0]
    print(mis)
    
    ms=m*n # max sum
    print(ms)
    
    for mi in mis:
        
        al=a[:mi]
        ad=a[mi:]
        if len(ad)>0 and len(al)>0:
            mal=max(al)
            mad=max(ad)
            ms=min(ms, mal*len(al)+mad*len(ad))
            print(1,al,ad,mal,mad,ms)
        
        if mi+1<n:
            mi+=1    
            al=a[:mi]
            ad=a[mi:]
            print(2,al,ad)
            if len(ad)>0 and len(al)>0:
                mal=max(al)
                mad=max(ad)
                ms=min(ms, mal*len(al)+mad*len(ad))
                print(1,al,ad,mal,mad,ms)

    return ms

LongestPassword

s = "zxcasdqwe123"

import re

def a(s):
    m = re.match(r"^[a-zA-Z0-9]+$", s)
    if(m==None):
        return False
    else: 
        return True
    
def l(s):
    l = re.findall(r'[a-zA-Z]', s)
    s = "".join(str(i) for i in l)
    print(len(s))
    return len(s)
    
def d(s):
    d = re.findall(r'[0-9]+', s) 
    s = "".join(str(i) for i in d)
    return len(s)
   

def solution(s):
    nws = []
    ws = s.split() 
    #print(ws)
    for w in ws:
        if a(w) and l(w)%2==0 and d(w)%2==1:            
            nws.append(w)        

    print(nws)
            
    if(len(nws)==0):
        return -1
    mx = max(set(nws), key=len)
    return (len(mx))

Casino

n,k =8, 0
n,k =18, 2
n,k =10, 10 

# ideal sequence
def iseq(n, k):
    z = k # zeros left
    s = ''
    while(n>2):
        if n%2==1:
            s=s+'1'
            n=n-1
        else:
            if(z>0):
                s=s+'0'
                n=n/2
                z=z-1
            else:                
                s=s+'1'*int(n-1)
                return s[::-1]
            
    if(n==2):
        s=s+'1'
        
    if(n==3):
        s=s+'11'        
        
    return s[::-1]



def solution(n,k):
    b = iseq(n, k)
    print(b)    
    return len(b)

solution(21, 2)

Number of countries

from pandas import DataFrame

l = [[5,4,4], [4,3,4], [3,2,4], [2,2,2], [3,3,4], [1,4,4], [4,1,1]]
lr = len(l)
lc = len(l[0])
print (DataFrame(l))
nl =  [[0 for j in range(lc)] for i in range(lr)]   

# recursive paint neighbors
def pn(i,j, c, lv):
    
    if(i<0 or j<0 or j>=lc or i>=lr): 
        return

    # don't paint already painted i,j 
    if(nl[i][j]!=0):
        return   
    
    # stop the recursion if 
    if(l[i][j]!=lv):
        return

    nl[i][j]= c
    
    pn(i+1, j, c, lv)
    pn(i-1, j, c, lv)
    pn(i, j+1, c, lv)
    pn(i, j-1, c, lv)
    
    return
    
# return next to paint
def rn(l):
    lr = len(l)
    lc = len(l[0])
    for i in range(lr):
        for j in range(lc):
            if l[i][j]==0:
                return(i,j)
    return None # nothing to paint

def solution(l):
    c=1 # country counter
    lv = l[0][0] # old value
    pn(0, 0, c, lv)

    while None!=rn(nl):
        i,j = rn(nl)
        c = c+1
        lv = l[i][j]
        pn(i,j, c, lv)

    return max(max(nl) )

m = solution(l)
DataFrame(nl)

Number Of Means

def amean(a):
    return int(sum(a)/len(a))
    
def solution(a,m):
    n=len(a)
    print(n)
    am=amean(a)
    print(am)
    c=0
    for k in range (1,n+1):
        for i in range(0, n-k+1):
            s=a[i:i+k]
            if amean(s)==m:
                c+=1
    return c

a,m= [2, 4, 0], 2
solution(a,m)

Shortest Complete List

In here we need to find the length of the shortest sublist with all elements inside.

def solution(a):
    n=len(a)    
    l=len(set(a))
    d=dict()
    m=n # maximal
    i=0 # ind
    
    while i<n: # till the end of the array
        d[a[i]]=True
        
        if len(d)==l:
            si=i # saved i
            d.clear()
            for j in range(i,-1,-1):
                d[a[j]]=True
                print(d)
                if len(d)==l:
                    d.clear()
                    break
            print(i,j)
            m=min(m,i-j+1)
            i=si
        else:
            i+=1
            
            
    return m
    
a= [2, 1, 1, 3, 2, 1, 1, 3]
solution(a)

Appendix

Primes

from functools import reduce

# find all the divisors
def divisors(n):    
    return set(reduce(list.__add__, 
                ([i, n//i] for i in range(1, int(n**0.5) + 1) if n % i == 0)))


# number of divisors
def nod(n):
    i=1
    d=0
    while(i*i<n):
        if n%i==0:
            d+=2
        i+=1
    if(i*i==n):
        d+=1
    return d

# prime number test
def prm(n):
    i=2    
    while(i*i<n):
        if n%i==0:
            return False
        i+=1
    return True

# returns how many times 
# n is divisible by 2 and 5
def div2and5(n):
    f= {2:0, 5:0}
    if n==0:
        return f
    while(n%2==0):
        f[2]+=1
        n = n/2
    while(n%5==0):
        f[5]+=1
        n = n/5
    return f

Counter

from collections import defaultdict
from collections import Counter
a = [3,3,4,2,3,3,34,5,6]
c = Counter(a)
print("c[3] = ", c[3])
print([(k,v) for k,v in c.items()])
print(c.most_common(1))
print(c.most_common(1)[0][1])

Random int

from random import randint
a = [randint(-10000, 10000) for p in range(0, 10000)] 
#−2,147,483,648..2,147,483,647

Random string

import random
s = [random.choice(['a', 's', 'df']) for p in range(0, 10)]
print(s)

Random shuffled

import random
a = [i for i in range(1, 50000+1)]
random.shuffle(a)

All factors

For 6 would be = [2,3]

def alf(n):
    i=2
    t = n
    f=[]
    while(t>1):
        if t%i==0:
            f.append(i)
            t = t/i
        else:
            i+=1
    
    return f

Find sign of increase and decrease in array

def fsid(a):    
    n = len(a)
    ida = [0]*n
    for i in range (1,n):
        if a[i-1]<a[i]:
            ida[i]=1
        elif a[i-1]==a[i]:
            ida[i]=0
        else:
            ida[i]=-1
    return ida
a=[1, 5, 3, 3, 4, 3, 4, 1, 2, 3, 4, 6, 2]
fsid(a)
# [0, 1, -1, 0, 1, -1, 1, -1, 1, 1, 1, 1, -1]

Find increase and decrease in array

def fid(a):
    n = len(a)
    ida = [0]*n
    for i in range (1,n):
        dif = a[i]-a[i-1]
        ida[i]=dif
    return ida
a=[1, 5, 3, 4, 3, 4, 1, 2, 3, 4, 6, 2]
fid(a)
#[0, 4, -2, 1, -1, 1, -3, 1, 1, 1, 2, -4]

Find peaks of array

def fp(a):
    n = len(a)
    p = [0]*n
    for i in range (1,n-1):
        if a[i-1] < a[i] and a[i]>a[i+1]:        
            p[i]=1
    return p

a=[1, 5, 3, 4, 3, 4, 1, 2, 3, 4, 6, 2]
fp(a)
#[0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0]

Even better peaks:

def peaks2(a):
    n=len(a)
    p=[0]*n #peaks
    if a[0]>a[1]:
        p[0]=1 # peak
    if a[-1]>a[-2]:
        p[-1]=1 # peak
        
    for i in range (1,n-1):
        if a[i-1]<a[i]>a[i+1]:
            p[i]=1
        if a[i-1] < a[i] and a[i]==a[i+1]:
            p[i]=1 #also peak
        if a[i-1] == a[i] and a[i]>a[i+1]:
            p[i]=1 # also peak
            
    return p

Find peak differences

def positions(a,el):
    d = [i for i,e in enumerate(a) if e==el]
    return d

a=[0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0]
positions(a,1)
#[0,2,2,5]

Prime numbers

def primes(n):    
    m = [1]* (n+1) # mask
    m[0] = m[1] = 0
 
    i = 2
    while (i*i <= n):
        if m[i] == 1:
            for j in range(i*i, n+1, i):
                m[j] = 0
        i += 1
 
    i = 2
    return m

print(primes(1000)[0:10])
# [0, 0, 1, 1, 0, 1, 0, 1, 0, 0]

GCD substract

def gcds(a,b):
    if a == b:
        return a
    if a > b:
        return gcds(a - b, b)
    else:
        return gcds(a, b - a)

GCD using %

def gcdm(a,b):
    if a%b==0:
        return b 
    else:
        return gcdm(b,a%b)

LCD based on GCD

def lcd(a,b):
    return a*b/gcds(a,b)

First 50 fibs

def fib(n=50):
    f = [0] * (n)
    f[1] = 1
    for i in range(2, n):
        f[i] = f[i - 1] + f[i - 2]
        
    return f
        
f = fib(n=50)
print(f, len(f))

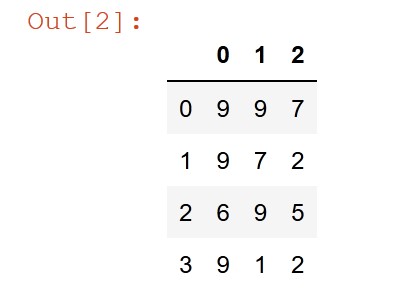
Nice looking matrix

import pandas as pd
a= [[9, 9, 7], [9, 7, 2], [6, 9, 5], [9, 1, 2]]
df = pd.DataFrame(a) 
df

matrix

Random matrix

from random import randint
a =  [[ randint(1, 9) for c in range(0, 10)] for r in range (0,10)] 
print(a)
import pandas as pd
df = pd.DataFrame(a) 
df

matrix

List contains another list

a, L = [2,2,5],[5, 8, 5, 15, 25]
# check if L contains a
def contains(L,a):
    l = L.copy()
    for e in a:
        try:
            l.remove(e)
        except:
            return False
    return True
contains(L,a)

Rotate matrix clockwise

m= [[1, 2, 3], [4, 5, 6], [7, 8, 9], [10,11,12]]
n = [[m[j][i] for j in range(len(m)-1,-1,-1)] for i in range(len(m[0]))]

Rotate matrix counterclockwise

m= [[1, 2, 3], [4, 5, 6], [7, 8, 9], [10,11,12]]
n = [[m[j][i] for j in range(len(m))] for i in range(len(m[0])-1,-1,-1)]

Transpose matrix

m= [[1, 2, 3], [4, 5, 6], [7, 8, 9], [10,11,12]]
n = [[m[j][i] for j in range(len(m))] for i in range(len(m[0]))]

Smart factorial

F=[1]

#smart factorial
def f(b):  
    global F
    n=len(F)
        
    while n<=b:
        F.append(n*F[-1])
        n+=1
    return F[b]

Number of combinations

# uses previous f function
def comb(n,k):
    return f(n) // (f(k)*f(n-k))

…

tags: problems - codility task solutions - logic - programming - Iterations - BinaryGap - Arrays - CyclicRotation - OddOccurrencesInArray - Time Complexity - PermMissingElem - FrogJmp - TapeEquilibrium - Counting Elements - FrogRiverOne - MaxCounters - MissingInteger - PermCheck - Prefix Sums - PassingCars - GenomicRangeQuery - MinAvgTwoSlice - CountDiv - Sorting - Triangle - Distinct - MaxProductOfThree - NumberOfDiscIntersections - Stacks and Queues - Brackets - Nesting - StoneWall - Fish - Leader - Dominator - EquiLeader - Maximum Slice Problem - MaxProfit - MaxSliceSum - MaxDoubleSliceSum - Prime and composite numbers - MinPerimeterRectangle - CountFactors - Peaks - Flags - Sieve or Eratosthenes - CountSemiprimes - CountNonDivisible - Euclidean Algorithm - ChocolatesByNumbers - CommonPrimeDivisors - Fibonacci Numbers - FibFrog - Ladder - Binary Search - MinMaxDivision - NailingPlanks - Caterpillar method - AbsDistinct - CountDistinctSlices - CountTriangles - MinAbsSumOfTwo - Greedy algorithms - TieRopes - MaxNonoverlappingSegments - Dynamic Programming - NumberSolitaire - MinAbsSum - Challenges - Buckets - SheepAndSunshades - Rivers - DifferentCharacters - DreamTeam - MaxPathFromTheLeftTopCorner - FloodDepth - MaxZeroProduct - TheaterTickets - Canoeist - BeautifulPassword - PascalTriangles - CoverBuildings - LongestPassword - Casino - Number of countries - Number Of Means - Shortest Complete List & category: python